【中３】数理探究「連分数の魅力」（宇都宮大学・鈴木先生）

９月１２日（月）、３・４限目、中学３年１組の「数理探究」（数学分野）の授業を見学しました。今日は、宇都宮大学共同教育学部の鈴木拓先生を講師にお迎えし、「連分数の魅力　～数当てゲームと近似のお話」というテーマで、数学の面白さを教えていただきました。なお、１・２限目は３年３組、５・６限目は３年２組で、同じ授業が実施されました。

授業は、まず、「連分数とは何か」から始まりました。

連分数とは、

・分数の分母に更に分数が現れるような式

・分子の数は全て１

これらを満たす分数です。

分子の数が分母より大きい分数を「過分数」といいますが、「過分数」は、下図のように簡単に「連分数」で表すことが出来ます。

実際に、いくつかの過分数を連分数に直してみました。できたら、周りの生徒同士で確かめました。

次は、「数当てゲーム」です。

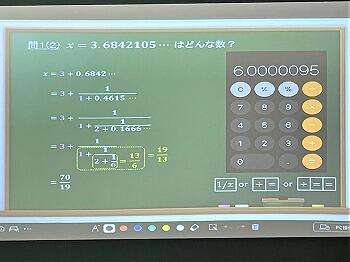
例えば、X＝3.6842105‥　という少数は、分数で表すとどんな数になるでしょう。これが「数当てゲーム」です。

「そんなこと当たりっこない」普通に考えれば、そう答えるでしょう。でも、「連分数」を使うと意外と簡単に出来るんです。ただし、電卓は使います。鈴木先生は、電卓の画面を示しながら、どのキーを押せばいいか、までわかりやすく丁寧に教えてくださいました。

実際に、いくつかの少数を分数で表しました。

合っているかどうか、生徒同士で確かめています。

もうだいぶわかってきました。だんだん楽しくなってきました。

次に、有理数と無理数を連分数で表すと、どのような違いがあるか、確かめました。無理数とは、√２のような数です。無理数は、連分数で表すと、無限に続き、終わりがありません。（これを無限連分数というそうです。）

２時間連続の授業の１時間目は、この辺りで終わりました。休み時間の後、後半へと続きました。

２時間目は「連分数による近似」です。

例えば、円周率（π＝3.1415926‥）は無理数ですので、分数で表すことはできませんが、連分数を使うと、近似する数で表すことが出来ます。ちなみに、円周率の１次近似は π ≒３、２次近似は π ≒ 22/7 （→7分の22です）、３次近似は π ≒ 333 / 106 （→106分の333です）

同様に、√３（≒1.7320508‥）や√５（≒2.360679‥）などの近似を連分数を使って求めました。

さらに、連分数を使うと、「１太陽年」の近似を求めることが出来ます。

「１太陽年」とは、地球が太陽の周りをぐるっと１周するのにかかる日数です。１年３６５日と言われていますが、実際は365.2421895‥という数値です。つまり、１年を３６５日とすると、４年で約１日分増えてしまいます。そこで、４年に１回、うるう年がやってくるのですが、これでもずれが生じるので、「１００年に１度、うるう年を例外で平年とする」、さらに「４００年に１度、例外の例外で、平年としないでうるう年とする」というルールがあります。

これを「グレゴリオ暦」といい、多くの地域で採用されています。

また、「イラン暦」というのもあり、「１２８年に１回、例外で平年」としています。

実は、「イラン暦」の方がより正確で、１太陽年を連分数で表したときの５次近似である365＋ 31/128 に基づいています。

＊こんな風に、日常生活の中に、連分数の考え方が息づいていることを知り、鈴木先生の特別授業は終わりました。大満足で、とても楽しい授業でした。「数学って面白いな」と感じてくれた生徒がたくさんいたことを期待しています。