文字
背景
行間
校長室便り
身近な風景 ~セミの抜け殻調査
8月3日付けの「身近な風景」では、「ミンミンゼミの謎」を紹介しました。
今年はやけにミンミンゼミの鳴き声が聞こえるのに、採取したセミの抜け殻は、ほとんどがアブラゼミで、ミンミンゼミのものは全くありませんでした。これが「ミンミンゼミの謎」でした。
この謎を解くため、「たまたま採取した抜け殻に、ミンミンゼミが含まれてなかっただけで、探せばミンミンゼミもでてくるのではないか」という仮説を立てました。
そこで、8月17日(始業式)と8月20日に、校庭の前庭から、セミの抜け殻をできるだけたくさん集めました。(掃除中に探索に協力してくれた生徒の皆さん、ありがとうございました。)
すると、2日間合わせて20分程度で、141個の抜け殻を採取しました。
これをセミの種類ごとに分けると、以下のようになります。

今年はやけにミンミンゼミの鳴き声が聞こえるのに、採取したセミの抜け殻は、ほとんどがアブラゼミで、ミンミンゼミのものは全くありませんでした。これが「ミンミンゼミの謎」でした。
この謎を解くため、「たまたま採取した抜け殻に、ミンミンゼミが含まれてなかっただけで、探せばミンミンゼミもでてくるのではないか」という仮説を立てました。
そこで、8月17日(始業式)と8月20日に、校庭の前庭から、セミの抜け殻をできるだけたくさん集めました。(掃除中に探索に協力してくれた生徒の皆さん、ありがとうございました。)
すると、2日間合わせて20分程度で、141個の抜け殻を採取しました。
これをセミの種類ごとに分けると、以下のようになります。

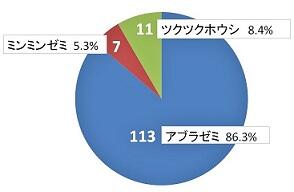
(1)種の構成
①アブラゼミ 113(オス52、メス61)


②ミンミンゼミ 7(オス3、メス4)

③ツクツクホウシ 11(オス7、メス4)

④触覚が取れていて種の判別不能(10)
*これらのことから、佐野高校の校庭でみられるセミの種構成は、やはり、アブラゼミが圧倒的に多いことがわかりました。これは、他の文献を調べてみても同様で、少なくとも関東近県で鳴いているセミは、アブラゼミが主力で、ミンミンゼミの数は非常に少ないようです。
アブラゼミの鳴き声は「ジーッ」と油を揚げているような音がすることから、アブラゼミという名前がついていますが、たくさん鳴いていても、「ジーッ」だけだと何匹ないているのかわからないのに対して、ミンミンゼミは、「ミーンミンミン…」と何匹が鳴いているかわかりやすいので、たとえ数が少なくても、たくさんいるように聞こえてしまうのかもしれません。
(これもあくまで仮説です。8月21日に微生物研究家の松葉君(中学1年2組)に相談したら、「ミンミンゼミの幼虫が、木の高いところで羽化したため、抜け殻が見つかりにくかった、という可能性がありますね。」という指摘がありました。確かにその可能性は否定できませんが、肉眼で確認できる高さ(2m程度)で捕獲できた抜け殻に限定して考えることにしました。)
(2)性比
次に、3種のセミのオスメスの性比に着目してみましょう。
セミのオスメスは、お尻にある突起の形で、簡単に判別できます。
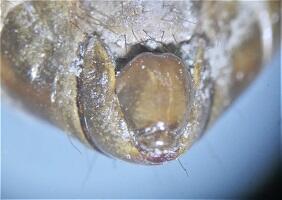
オス(おしりの突起が一つだけ)

メス(おしりの突起が2つある)
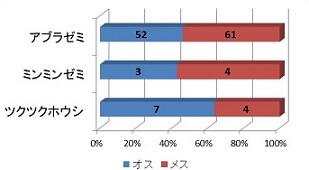
採取数では、アブラゼミとミンミンゼミはメスが多く、ツクツクホウシはオスが多い結果です。それはそれでいいのですが、例えば、「アブラゼミは、佐野高校ではメスの方が多くいる」あるいは、「ツクツクホウシは、佐野高校ではオスの方が多くいる」と言い切ってしまっていいのでしょうか。
可能性としては、①本当はオスメス同じくらいいて、たまたまメス(オス)の抜け殻を多く採取した(雌雄同数)、②実際に、メス(オス)の方がオス(メス)よりも多くいる。→性比がメス(オス)に偏っている、の2つが考えられます。
実は、これを証明するのは割と簡単なんです。高校の数学で統計解析について勉強しますが、それを応用すれば、求めることが出来ます。私は、数学が専門ではありませんが、統計というのは、文系理系を問わず、研究する際に必要になってきます。ここでは「性比に有意性があるか」を調べることにします。
例えば、佐野高校の校庭に「アブラゼミはオスメス同数いる」と仮説を立て、そのアブラゼミの集団から、10匹を捕まえた時のオスメスの性比の可能性は、以下の表のようになります。
オスメスの捕獲のしやすさは同じとして、捕まえた10匹中、オスが10匹や9匹というのはめったに起こらない、というのはなんとなくわかりますよね。逆に、メスが9匹や10匹というのもめったに起こりません。といっても、その可能性はゼロではありません。
そこで、100回やって5回以上起こる確率があるか、5回は無理でも1回でも起こる確率があるかで、線引きをして、「オスとメスが同数いる」という仮説が正しいか、間違っているかを判断します。
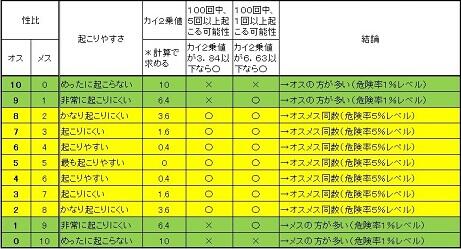
それには、「カイ2乗値」というのを計算して、その数値で、仮説がどの程度当てはまるかを判断します。計算の仕方は難しくありません。エクセルでもできます。(とりあえず、そういうものがありますということで構いません。)
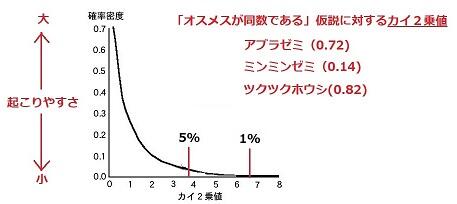
実際に、アブラゼミ、ミンミンゼミ、ツクツクホウシの「カイ2乗値」を計算すると、アブラゼミは0.72、ミンミンゼミは0.14、ツクツクホウシは0.82となり、上のグラフの横軸の値でみてみると、5%の値(3.84)以下ですので、「オスメス同数」という仮説が、ある程度「起こりやすい」ことがわかります。
このことから、佐野高校にいる3種は、それぞれ「オスメス同数である」という仮説を否定できないことになります。そのため、「アブラゼミの抜け殻の数はメスの方が多かったが、有意にメスが多いとは言えない」→「(危険率5%レベルで)ほぼ同数である」ということが言えることになります。
*ちょっとメンドクサイ話でしたが、なぜ、こんなことを話したかを補足します。
皆さんは、課題研究で、様々な実験や観察、調査(アンケートなど)を行いますが、その時の結果で、たまたま、こちらの数が多かったから、こういう傾向がある、と判断してしまうことがよくあります。でも、その数値は、誤差を含んでいたり、たまたまそうだったのかもしれません。あるいは、本当にそういう結果だったという可能性もあります。
*そんな時、統計解析(例えば、「有意差の検定」)を使えば、仮説が間違ってないかどうかを数学的に証明することもできます。これは、論文を書く際には、強力な武器になります。なにしろ、数学的に証明されているんですから、説得力が違います。
*こういうこともできる、ということを頭の片隅に置いておいてくださいね。数学って役に立っているんです。
(数学の先生、説明に間違いがあったら教えてください。訂正します。)
緊急情報
特にありません。
カウンター
0
9
8
5
4
8
7
7







