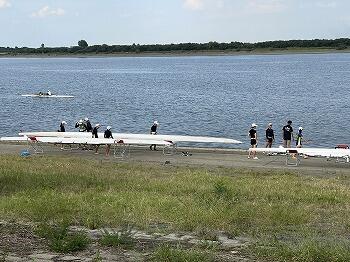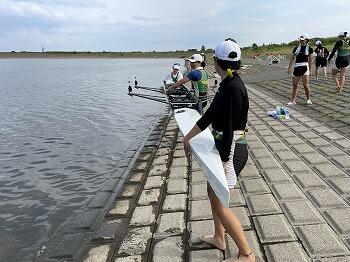文字
背景
行間
2022年9月の記事一覧
【中高】中高の全国大会の好成績を佐野市長に報告
【中高】「将棋全国大会」好成績の紹介記事
9月14日(水)・15日(木)、中学3年の石原橙真君と高校3年の竹熊柊君に関する記事が、連日、下野新聞で紹介されました。
9月15日付け下野新聞より(HP掲載許諾済)
【高校】第1回SG(Sano グローカル)教養講座
9月17日(土)午前中、「第1回SG(Sano グローカル)教養講座(5講座)」を開講しました。本講座は、SGH終了後の令和3年度から「Sano グローカル構想」の一環としてスタートしました。各分野の第一人者を講師にお招きし、本物に触れることで、今、日本でどんなことが起こっているのか、何が課題なのかを知ってもらうことをねらいとしています。
今回の講座の講師として、以下の5名の先生方にご講演いただきました。
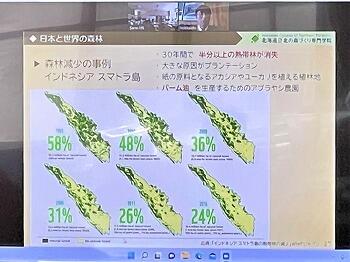
1 北海道立北の森づくり専門学校
主査:佐々木健人先生
2 日本両棲類研究所
所長:篠崎尚史先生
3 中央AI専門学校開校準備室
特別顧問:鈴木壮治先生
4 一般社団法人えんがお
代表:濱野将行先生
5 (株)時事通信出版出版事業部
部長:坂本健一郎先生
本日は、以下の日程で行われました。生徒(高校1,2年生は全員、高校3年生は希望者のみ)は希望する講師の講演に参加しました。
①講演(質疑応答含む)
9:00~10:30(90分間)
②振り返り記入(スマホ等)
10:30~10:45(15分間)
③休憩・移動
10:45~11:00
④課題研究指導(交流会)
11:00~11:45(45分間)
まずは、各講座の「講演」の様子です。
1 北海道立北の森づくり専門学校・佐々木健人先生(北海道からオンライン、生物室、36名受講)
2 日本両棲類研究所長・篠崎尚史先生(選択3教室、45名受講)
3 中央AI専門学校開校準備室特別顧問・鈴木壮治先生(旭城ホール、69名受講)
4 一般社団法人えんがお代表・濱野将行先生(英語演習室、63名受講)
5 (株)時事通信出版出版事業部部長・坂本健一郎先生(選択4教室、73名受講)
各講座終了後、講師の先生3名のご厚意により、生徒の課題研究について、アドバイス等をいただく「交流会」(選択3教室)が行われました。ここでは、講師の先生の専門分野に関連する生徒の「課題研究班」が、直接ご指導をいただきました。
*各講座のさわりだけしか観ることが出来ませんでしたが、どの講座も、各分野の最先端の研究や事業に関する興味深いお話でした。生徒の課題研究を深める上で、大きな刺激を受けたのではないかと思います。とても有意義な「SG教養講座」でした。
【高校】ボート部、谷中湖特設コースでの練習
9月17日(土)午後、とちぎ国体の会場である「谷中湖特設ボートコース」での練習を見学・応援に行きました。ボート部は、来たる国体(10月1日~4日)に向けて、9月16日(金)~19日(月)にかけて、現地で合宿を行っています。
少年女子クオドルプル(佐高3名:堀越紅羽、藤倉望妃、藤倉麻妃+佐野東高2名の栃木県チーム)
「谷中湖特設ボートコース」は、渡良瀬遊水地にある谷中湖に設置されています。ボート競技は、写真の白丸の辺りで行われます。矢印の方向から見ています。普段の「渡良瀬川特設コース」とは異なり、広い湖ですので、湖岸から見るとかなり遠くで漕いでいる感じがします。
本校から国体ボート競技に出場する種目と選手は以下の通りです。女子ダブルスカルは本校生コンビですが、他の種目は佐野東高校ボート部との「オール栃木」最強チームを編成しています。
少年女子ダブルスカル
S福地琴美(2年1組)
B高瀬綾乃(2年2組)
少年男子ダブルスカル
S青木瑛久(3年3組)
少年女子クォドルプル
S藤倉望妃(3年3組)
3堀越紅羽(3年3組)
B藤倉麻妃(3年2組)
少年男子クォドルプル
S清水雅裕(2年4組)
3宋 佳修(1年4組)
2船田佳佑(2年2組)
B三田翔愛(1年2組)
そして忘れてはならないのが、‥
成年女子シングルスカル
増田 萌(教諭)
谷中湖では桟橋がないので、湖からボートを引き上げるのが一苦労です。湖岸はぬるぬるして、つるっと滑りそうです。しかし、ここで転倒したら大変なことになりますので、皆、集中しています。
今日は、朝9時から15時過ぎまで、ひたすら漕ぐ練習を続けてきました。
疲れている中にも、笑顔が絶えません。3年生の4人です。
そして、1,2年生と増田先生です。
最後に、テントを撤収し、ボートを艇庫まで運びます。
栃木県の艇庫は、ここから歩いて20分くらいのところにあるそうです。
練習は、19日(月)まで続きますが、台風の影響が心配です。
明日は体育館での練習になるかもしれないそうですが、頑張ってください。応援しています。
PS :増田先生から合宿中の一コマの写真をいただきました。
宿泊先は「古河スポーツ交流センター」のようです。かなり大きな施設という感じがします。
17日(土)の午前練の後の昼休みです。テントの中で休んでいます。
昼休みの気だるい雰囲気が背中から伝わってきます。午後練もよく頑張りました。
「正々堂々」ハイヒールをはいたお坊さん
9月14日(水)15時、「一向寺」(佐野市堀米町)の住職である 東 公章さんが来校し、一冊の本を贈呈してくださいました。
「正々堂々 私が好きな私でいきていいんだ」ハイヒールをはいたお坊さん西村宏堂さんのご著書です。西村さんは、8月25日に佐野市で講演をしてくださいましたが、実は、本校の「第3の制服」が、実現の「きっかけ」となっていました。
(右側)佐野市の人権・男女共同参画課(人権推進係)の亀山さん
西村宏堂さんは、僧侶で、メイクアップアーティスト、LGBTQでもある独自の視点で「性別も人種も関係なく皆平等」というメッセージを発信しています。
1989年東京生まれの西村さんは、ニューヨークのパーソンズ美術大学を卒業。ミス・ユニバース世界大会やNYファッションウィークなどで、メイクを行い、世界的に高い評価を得ています。2021年にTIME誌「Next Generation Leaders」に選出されました。
ニューヨーク国連本部やイェール大学、増上寺などで講演を行い、その活動は、NHKやBBC(英国放送協会)など、国内外の多くのメディアに取り上げられています。現在は、ロンドンを拠点に活躍されているそうです。
そのような多忙な西村さんが、先月25日、佐野市文化会館で、「ハイヒールを履いた僧侶から学ぶ、自分に自信をもつ方法」と題するオンライン講演をしてくださいました。
西村さんは、現在では、お坊さんとしてお経を唱えて、メイクもして、ハイヒールも履き、キラキラのイヤリングもつけて、同性愛者であると公言されています。しかし、堂々と胸を張って自分のことを話せるようになったのは26歳からで、それまで周囲の人たちと違うセクシュアリティを隠し続けてきたそうです。特に高校3年間は「暗黒の谷」で、心を許せる友だちはひとりもできませんでした。
西村さんは、本校が昨年度、生徒たちによって「第3の制服」を導入し、自由に選べる制服となったことを知り、感銘を受けたそうです。そして、そのような高校のある「佐野市」でならと、御多忙な中、講演を引き受けてくださいました。意外な縁がありました。
皆さんの行動が、皆さんが知らないところで、気づかないうちに、西村さんを、そして社会をも動かしていたことを知りました。西村さんから、皆さんにも是非、読んでいただきたいと、自伝的な著書である「正々堂々 私が好きな私でいきていいんだ」を贈呈してくださいました。それを届けるために、同じ宗派の住職である東さん、そして、佐野市の人権推進係の亀山さんが、本日、校長室まで来てくださいました。この本は、図書室に置いておきますので、是非、手に取って、読んでみてください。
【中1】ホットケーキ作り(家庭科・保科先生)
9月14日(水)5限目、中学1年3組の「家庭科」の授業(保科先生)を見学しました。今日は、調理実習で「ホットケーキ」を作っていました。
おいしそうにできました。
最初に、保科先生から、材料や調理方法、注意点などについて、お話がありました。
生徒は、班ごとに必要な材料を取りに来ています。
続いて、材料を混ぜ合わせて、ホットケーキの生地を作ります。
いよいよ、フライパンで焼きます。今の生徒は、ガスを使っていない家庭もあるので、ガスで火を付けるという経験があまりないようです。先生や友達に教わりながら、やっていました。
フライ返しでひっくり返します。
焼き上がりました。完成です。
出来上がったホットケーキは、被服室に持って行って、対面にならないように食べました。
「ふわふわでおいしい」といった感想が聞かれました。自分で作ったとあれば、なおさらですね。
これで、ホットケーキというレパートリーが加わりました。
家でも作ってみてください。
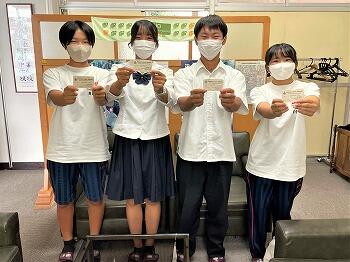
【高校】ボート部、「表彰カード」差し上げました。
9月13日(火)昼休み、インターハイで活躍したボート部の3年生4人が校長室に来てくれたので、前から渡す予定だった「表彰カード」を差し上げました。喜んでもらえて嬉しいです。
「表彰カード」は、飛駒和紙で作った特注品です。
【高3】「英語表現Ⅱ」の授業見学(久保田先生)
9月12日(月)7限目、高校3年1・2組の「英語表現Ⅱ」の授業(久保田先生)を見学しました。「読解力と表現力を高めるSDGs英語長文(三省堂)」というテキストを使って、Lesson 7 (Goal 7) 「ARRORDABLE AND CLEAN ENERGY エネルギーをみんなに そしてクリーンに」で、ウクライナのチェルノブイリ原発事故に関する長文に取り組んでいました。
気づいた人もいるかもしれませんが、このテキストは17のLesson からできており、それぞれが、SDGsの17のGoal に対応する長文(課題等)を扱っています。
チェルノブイリ原発事故は、1986年4月25日に発生し、翌26日、原子炉は暴走し、水蒸気爆発を起こして破壊され、大量の放射性物質が大気中に放出されました。その結果、現在もなお、原発から半径30キロ以内の地域での居住が禁止されています。
赤い部分が現在のウクライナ。その北はベラルーシ。
テキストでは、事故の様子や現状などについても紹介されています。そうした長文の英文をもとに、生徒たちは読解したり、表現したりしていました。また、お互いに英文を読んで、意味を説明していました。皆、意欲的に取り組んでいる姿が印象的でした。
今日のLessonのまとめとして、当時のチェルノブイリの原発事故に関する証言のインタビューなどを動画で視聴しました。
最後は、時間まで「聞き取り」が行われました。
*SDGsに関する大学入試の出題も多く、関連するテーマを理解したり、よく出てくるキーワードを知ることは、英語と時事的な勉強の両方を兼ねている素晴らしい受験勉強だと思いました。
また、今回のウクライナでのチェルノブイリ原発事故は、現在進行中のロシアの侵略の中で、原発が重要な位置を占めていることを改めて学ぶ、絶好の機会でもあります。「英語表現」の授業もシンカしていることを実感しました。
SDGsの他のGoal についても、どんな内容を扱うのか、興味を持ちました。
【中学】全国中学生英語ディベート大会(練習)
9月12日(月)放課後、「第12回 全国中学生英語ディベート大会」(9月25日、オンライン開催)に向けた練習を見学しました。6月頃、中学3年生を対象に参加希望者を募り、夏休み中などに定期的に練習を重ね、現在は、来週末の大会に向けた「最終調整」をしています。
集まった7名の有志生徒(相澤勇太君、浅田優君、井本宙汰君、黒澤さくらさん、朴正勲君、村田桜彩さん、山口紗季さん)
大会では、4試合を行いますが、そのうち3試合は準備型(論題:日本は中学生以下のスマートフォンなどの使用を禁止すべきである。是か非か)で、1試合は即興型です。夏休み中は、準備型での練習を積んできましたので、現在は、何が出るか分からない即興型の練習を繰り返しています。
ちなみに、今日の練習のお題は、
「中高生にとって、ボーイフレンドやガールフレンドを持つことは、時間の無駄である。是か非か」でした。
このお題が出るかどうかはわかりませんが、とにかく、お題が発表されたら、15分間で、それぞれの立場(是か非か)の論理構成を考えなければなりません。さらに、それを相手に英語で伝えなければなりません。そう簡単なことではありません。しかし、生徒たちは整然と、それぞれの役割を果たし、スピーチしていました。
*これまで練習を積んできたせいか、ちょっとやそっとでは動じない、安定感が感じられました。チームとしての目標もあるようですが、順位にはこだわらず、英語ディベートを楽しんで欲しいと思います。応援しています。
【中3】数理探究「連分数の魅力」(宇都宮大学・鈴木先生)
9月12日(月)、3・4限目、中学3年1組の「数理探究」(数学分野)の授業を見学しました。今日は、宇都宮大学共同教育学部の鈴木拓先生を講師にお迎えし、「連分数の魅力 ~数当てゲームと近似のお話」というテーマで、数学の面白さを教えていただきました。なお、1・2限目は3年3組、5・6限目は3年2組で、同じ授業が実施されました。
授業は、まず、「連分数とは何か」から始まりました。
連分数とは、
・分数の分母に更に分数が現れるような式
・分子の数は全て1
これらを満たす分数です。
分子の数が分母より大きい分数を「過分数」といいますが、「過分数」は、下図のように簡単に「連分数」で表すことが出来ます。
実際に、いくつかの過分数を連分数に直してみました。できたら、周りの生徒同士で確かめました。
次は、「数当てゲーム」です。
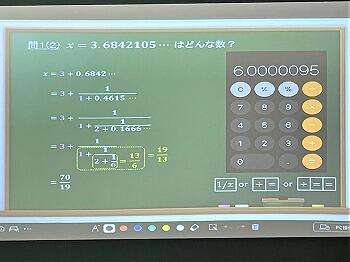
例えば、X=3.6842105‥ という少数は、分数で表すとどんな数になるでしょう。これが「数当てゲーム」です。
「そんなこと当たりっこない」普通に考えれば、そう答えるでしょう。でも、「連分数」を使うと意外と簡単に出来るんです。ただし、電卓は使います。鈴木先生は、電卓の画面を示しながら、どのキーを押せばいいか、までわかりやすく丁寧に教えてくださいました。
実際に、いくつかの少数を分数で表しました。
合っているかどうか、生徒同士で確かめています。
もうだいぶわかってきました。だんだん楽しくなってきました。
次に、有理数と無理数を連分数で表すと、どのような違いがあるか、確かめました。無理数とは、√2のような数です。無理数は、連分数で表すと、無限に続き、終わりがありません。(これを無限連分数というそうです。)
2時間連続の授業の1時間目は、この辺りで終わりました。休み時間の後、後半へと続きました。
2時間目は「連分数による近似」です。
例えば、円周率(π=3.1415926‥)は無理数ですので、分数で表すことはできませんが、連分数を使うと、近似する数で表すことが出来ます。ちなみに、円周率の1次近似は π ≒3、2次近似は π ≒ 22/7 (→7分の22です)、3次近似は π ≒ 333 / 106 (→106分の333です)
同様に、√3(≒1.7320508‥)や√5(≒2.360679‥)などの近似を連分数を使って求めました。
さらに、連分数を使うと、「1太陽年」の近似を求めることが出来ます。
「1太陽年」とは、地球が太陽の周りをぐるっと1周するのにかかる日数です。1年365日と言われていますが、実際は365.2421895‥という数値です。つまり、1年を365日とすると、4年で約1日分増えてしまいます。そこで、4年に1回、うるう年がやってくるのですが、これでもずれが生じるので、「100年に1度、うるう年を例外で平年とする」、さらに「400年に1度、例外の例外で、平年としないでうるう年とする」というルールがあります。
これを「グレゴリオ暦」といい、多くの地域で採用されています。
また、「イラン暦」というのもあり、「128年に1回、例外で平年」としています。
実は、「イラン暦」の方がより正確で、1太陽年を連分数で表したときの5次近似である365+ 31/128 に基づいています。
*こんな風に、日常生活の中に、連分数の考え方が息づいていることを知り、鈴木先生の特別授業は終わりました。大満足で、とても楽しい授業でした。「数学って面白いな」と感じてくれた生徒がたくさんいたことを期待しています。
特にありません。