文字
背景
行間
校長室便り
校長室便り
中3(家庭科)の授業見学
今日の1限目、中学3年2組の「技術家庭(家庭)」の授業(森戸先生)を見学しました。
「保冷バックの製作(全6時間)」の3時間目ということで、今日は以下のような作業をしていました。(白板に今日やることがわかりやすく書かれています。)
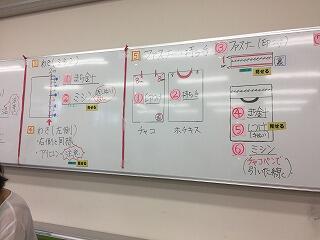
「保冷バックの製作(全6時間)」の3時間目ということで、今日は以下のような作業をしていました。(白板に今日やることがわかりやすく書かれています。)

①色のついた布の右側のわき1.5cm幅でチャコで印をつけ、アイロンで折り目をつけ、内側にアルミ布はさみます。
②ぬいしろに、まち針をさして固定し、ミシンで縫います。→見せる
③左側のわきも右側と同様に、1.5cm幅で印をつけ、アイロンで折り目をつけます。→見せる
④持ち手をつける場所に印をつけ、持ち手をホチキスで仮止めします。
⑤ファスナーを縫い付ける場所に印をつけます。→見せる
この →見せるというのが、森戸先生のオリジナルな指導法で、間違い易いところを未然に防ぐことができます。
このチェックポイントごとに先生に見せに来て、合格をもらうと自分ではんこを押し、次の作業に進みます。これによって、誰もが間違いなく完成することができるのだそうです。
(余談)色のついた布は5色(黒、青、ベージュ、ピンク、黄色)あり、希望で選べます。
今年の一番人気は「黒」で、次が「青とベージュ」だそうです。

チェックポイントを確認してもらいます。

合格したら、自分ではんこを押します。
生徒たちは、お互いに教わったりしながら、もくもくと作業を進めていきます。
自分が何をすればいいのかよくわかっている、という感じでした。ミシンの調子が悪い時は、自分で何とかしていました。




完成するには、あと3時間分の作業が必要です。得意不得意はあるようですが、一人一人着実に進んでいることは間違いないようです。りっぱですね。
授業終了後、生徒にどこが難しかったのか聞いてみました。
安藤さん「アイロンでわきの折り目をつけるとき、温度が高いとアルミが溶けてしまうので、どうやってアイロンをかけるかが難しかったです。」
清水君「まち針を指すのが難しかったです。ミシンをかけるとき、少ししわができてしまいましたが何とかできました。」
*完成したら、お弁当を入れて持ってきます、と多くの生徒が答えてくれました。自分で使うものを自分でつくる。
「素晴らしい」としかいいようがありません。
校長室(自宅)便り⑨ ~有理数と無理数(再考)
先日(26日)、中3の数学の授業(服部先生)を見せてもらいましたが、その際、そもそも、なぜ分数で表すことが出来る数を「有理数」というのかが、大変気になりました。有理数の理は、何を意味しているのでしょうか?
気になると眠れなくなりそうなので、本日(28日)、佐野市立図書館で、有理数に関して解説している本がないかどうか、探してみました。
そしたら、あったのです! しかも、2冊も。
①桜井 進「面白くて眠れなくなる数学」(2010年8月、PHP出版)
→著者は、東京工業大学理学部数学科卒業、同大学院卒業の「サイエンス・ナビゲーター」。世界初の「数学エンターテイメント」で話題、という有名人です。期待大ですね。気になって眠れないのと、面白くて眠れないのと、どっちを取るかです。
②一松 信「数の世界 -概念の形成と認知」(2015年1月、丸善出版)
→著者は1926年生まれ、京都大学名誉教授です。著書の冒頭で「数って一体何なのだろう?」と考えたことはありませんか? と投げかけています。完全に学者の先生ですので、より学問的な裏付けがわかるかもしれません。こちらも期待できそうです。

気になると眠れなくなりそうなので、本日(28日)、佐野市立図書館で、有理数に関して解説している本がないかどうか、探してみました。
そしたら、あったのです! しかも、2冊も。
①桜井 進「面白くて眠れなくなる数学」(2010年8月、PHP出版)
→著者は、東京工業大学理学部数学科卒業、同大学院卒業の「サイエンス・ナビゲーター」。世界初の「数学エンターテイメント」で話題、という有名人です。期待大ですね。気になって眠れないのと、面白くて眠れないのと、どっちを取るかです。
②一松 信「数の世界 -概念の形成と認知」(2015年1月、丸善出版)
→著者は1926年生まれ、京都大学名誉教授です。著書の冒頭で「数って一体何なのだろう?」と考えたことはありませんか? と投げかけています。完全に学者の先生ですので、より学問的な裏付けがわかるかもしれません。こちらも期待できそうです。

①桜井 進「面白くて眠れなくなる数学」からわかったこと
・先日の服部先生の授業では、有理数の例として、分数 22/7 がさりげなく登場していましたが、実は深い意味があったようです。世界の「7月22日」は「円周率の日」とされていて、22/7 (22÷7)を計算すると、3.142…となり、円周率の近似値になっています。紀元前250年、ギリシャの数学者アルキメデスが、世界で最初に円周率を計算によって、22/7と求めました。そのことを記念して、7月22日は「円周率の日」と制定されているのです。
円周率は紀元前二千年前から探究されてきましたが、その値は長い間、分数で表されていました。小数が発明されたのは今から400年前に過ぎないのです。
(→ちなみに、日本の「円周率の日」は3月14日。わかりやすすぎますね!)
・ところで、日本では「分数で表すことが出来る数」を「有理数」と呼んでいますが、英語で「有理数」は何と呼ばれているのでしょうか?英訳すると「Rational Number」となるそうです。形容詞「Rational」の名詞形は「Ratio」で、「Ratio」とは「比」を表しています。つまり、形容詞「Rational」は「比なる数」という意味になります。つまり、分数は分子と分母の数の比なので、「比なる数」だというのです。
しかし、それだったら、日本人が「Rational Number」を日本語に訳すとき、「有理数」ではなく「有比数」とすればよかったのではないでしょうか。
(→これって、誤訳だったの?)
・著者は、ここからさらにもう一歩踏み込みます。実は、英語の「Ratio」の起源となったラテン語の「Ratio」には「計算」という意味があるのです。「計算すること」から「比」に通じ、「Rational」は「計算的な」となり「合理的な」になっていきました。そうすると、「Rational Number」の日本語訳の候補として、「比なる数→有比数」と「合理的な数」すなわち「理が有る数→有理数」の2つあったのに、「有理数」が採用されたことになります。なぜ、後者に軍配があがったのでしょうか?
(→さすがはサイエンス・ナビゲーターですね。理詰めで畳みかけてきます。)
・「ピタゴラスの定理」で有名な、古代ギリシャの数学者ピタゴラス(紀元前6世紀頃)は、「万物の根源は数なり」と言ったと伝えられています。この「数」とは自然数(正の整数)のことです。ピタゴラスの時代、自然数こそが計算できる数、つまり「理性の象徴」というべき存在ととらえられていました。分数は、二つの自然数の比として考えられる(計算できる)数に他ならず、そうでない数は「非合理的な」という意味となり、排斥されるべき「考えてはいけない存在」だったというのです。そうした歴史的な背景を考慮し、「Ratinal Number」を「有理数」と訳したのではないか、というのが著者の説です。
(→なるほど、説得力ありますね)
・一方、「無理数」の概念は、もっと後になってから出てきます。現代では、√2やπ(円周率)が無理数であることは知られています。しかし、無理数であること(=分数では表すことが出来ないこと)を証明することは、そう簡単ではありませんでした。円周率πが無理数であることが証明されたのは1761年になってからのことでした。400年前、小数点が発明されたことで、ようやく分数を超えて「無理数」への挑戦が始まったのです。
(→確かに、有理数と無理数はセットになっていますので、「無理数」が存在することがわかって、初めて「有理数」という概念が生じてきたのですね。)
・無理数の英訳は「Irrational Number」で、打消しの接頭語Irがついているので、「比に非ず」と「非合理的」の意味があります。この英語を始めて日本語に訳した昔の日本人数学者は、「非合理的」を採用して、「無理」という言葉をあてたのではないか。
(→個人的には、著者の考えに深く納得しました。)
②一松 信「数の世界」からわかったこと
・こちらの著者は、「有理数」について、以下のように断言します。
「ピタゴラスは半ば伝説的な人物ですが、その伝統もあって古代ギリシャでは当初すべての数は互いに整数の比で表わされる、つまり整数の比で表される分数だけで十分と考えていました。今日では整数の比で表される数を「有理数」といいます。これはRational Number の訳語ですが、原義は「ratio(比)をもつ数」の意味で、むしろ「有比数」と呼ぶのが的確でした。しかし、すでにこの語が定着しているので、厳格にいえば「誤訳」ですがそのまま使います。」と述べています。
(→つまり、昔の日本人数学者が訳した言葉なので、なぜそのように訳したのかを詮索してもしようがない。それは、学問的にはさして重要なことではない。ということでしょうか。なるほど、学者としては、そのように考えるものなのかもしれませんね。)
・しかし、この本には、√2が無理数であることの証明や、なぜ、0.9999999…=1なのか、の証明が詳しく紹介されています。先日の服部先生の授業では、0.9999999…=1が正しいのかどうかわかりませんでしたが、この本では、0.99999999…=1 であることを証明しています。てっきり間違いだと思っていましたが、数学的に正解でした。それを知れただけでも、この本を読んだ価値がありました。
(→もっとも、全部は読んでませんけどね。興味あるところだけです。文献調査をする際は全部読む必要は全くありません。)
*最後に一言。これらはいわゆる「文献調査」です。たった2冊の本でしたが、その主張は微妙に異なっていましたね。
*自分にとって、どちらがより納得するか、という見方はありますが、どちらが正しいとは判断できません。文献調査をする際は、最低でも複数の文献にあたらないと危険です。文献調査で間違ったことをうのみにしてしまうと、そもそも前提から間違った方向に研究が進んでしまう可能性があるからです。
*少なくとも、「諸説あります」くらいの知識がないと、「チコちゃんに叱られますよ!」
①桜井 進「面白くて眠れなくなる数学」からわかったこと
・先日の服部先生の授業では、有理数の例として、分数 22/7 がさりげなく登場していましたが、実は深い意味があったようです。世界の「7月22日」は「円周率の日」とされていて、22/7 (22÷7)を計算すると、3.142…となり、円周率の近似値になっています。紀元前250年、ギリシャの数学者アルキメデスが、世界で最初に円周率を計算によって、22/7と求めました。そのことを記念して、7月22日は「円周率の日」と制定されているのです。
円周率は紀元前二千年前から探究されてきましたが、その値は長い間、分数で表されていました。小数が発明されたのは今から400年前に過ぎないのです。
(→ちなみに、日本の「円周率の日」は3月14日。わかりやすすぎますね!)
・ところで、日本では「分数で表すことが出来る数」を「有理数」と呼んでいますが、英語で「有理数」は何と呼ばれているのでしょうか?英訳すると「Rational Number」となるそうです。形容詞「Rational」の名詞形は「Ratio」で、「Ratio」とは「比」を表しています。つまり、形容詞「Rational」は「比なる数」という意味になります。つまり、分数は分子と分母の数の比なので、「比なる数」だというのです。
しかし、それだったら、日本人が「Rational Number」を日本語に訳すとき、「有理数」ではなく「有比数」とすればよかったのではないでしょうか。
(→これって、誤訳だったの?)
・著者は、ここからさらにもう一歩踏み込みます。実は、英語の「Ratio」の起源となったラテン語の「Ratio」には「計算」という意味があるのです。「計算すること」から「比」に通じ、「Rational」は「計算的な」となり「合理的な」になっていきました。そうすると、「Rational Number」の日本語訳の候補として、「比なる数→有比数」と「合理的な数」すなわち「理が有る数→有理数」の2つあったのに、「有理数」が採用されたことになります。なぜ、後者に軍配があがったのでしょうか?
(→さすがはサイエンス・ナビゲーターですね。理詰めで畳みかけてきます。)
・「ピタゴラスの定理」で有名な、古代ギリシャの数学者ピタゴラス(紀元前6世紀頃)は、「万物の根源は数なり」と言ったと伝えられています。この「数」とは自然数(正の整数)のことです。ピタゴラスの時代、自然数こそが計算できる数、つまり「理性の象徴」というべき存在ととらえられていました。分数は、二つの自然数の比として考えられる(計算できる)数に他ならず、そうでない数は「非合理的な」という意味となり、排斥されるべき「考えてはいけない存在」だったというのです。そうした歴史的な背景を考慮し、「Ratinal Number」を「有理数」と訳したのではないか、というのが著者の説です。
(→なるほど、説得力ありますね)
・一方、「無理数」の概念は、もっと後になってから出てきます。現代では、√2やπ(円周率)が無理数であることは知られています。しかし、無理数であること(=分数では表すことが出来ないこと)を証明することは、そう簡単ではありませんでした。円周率πが無理数であることが証明されたのは1761年になってからのことでした。400年前、小数点が発明されたことで、ようやく分数を超えて「無理数」への挑戦が始まったのです。
(→確かに、有理数と無理数はセットになっていますので、「無理数」が存在することがわかって、初めて「有理数」という概念が生じてきたのですね。)
・無理数の英訳は「Irrational Number」で、打消しの接頭語Irがついているので、「比に非ず」と「非合理的」の意味があります。この英語を始めて日本語に訳した昔の日本人数学者は、「非合理的」を採用して、「無理」という言葉をあてたのではないか。
(→個人的には、著者の考えに深く納得しました。)
②一松 信「数の世界」からわかったこと
・こちらの著者は、「有理数」について、以下のように断言します。
「ピタゴラスは半ば伝説的な人物ですが、その伝統もあって古代ギリシャでは当初すべての数は互いに整数の比で表わされる、つまり整数の比で表される分数だけで十分と考えていました。今日では整数の比で表される数を「有理数」といいます。これはRational Number の訳語ですが、原義は「ratio(比)をもつ数」の意味で、むしろ「有比数」と呼ぶのが的確でした。しかし、すでにこの語が定着しているので、厳格にいえば「誤訳」ですがそのまま使います。」と述べています。
(→つまり、昔の日本人数学者が訳した言葉なので、なぜそのように訳したのかを詮索してもしようがない。それは、学問的にはさして重要なことではない。ということでしょうか。なるほど、学者としては、そのように考えるものなのかもしれませんね。)
・しかし、この本には、√2が無理数であることの証明や、なぜ、0.9999999…=1なのか、の証明が詳しく紹介されています。先日の服部先生の授業では、0.9999999…=1が正しいのかどうかわかりませんでしたが、この本では、0.99999999…=1 であることを証明しています。てっきり間違いだと思っていましたが、数学的に正解でした。それを知れただけでも、この本を読んだ価値がありました。
(→もっとも、全部は読んでませんけどね。興味あるところだけです。文献調査をする際は全部読む必要は全くありません。)
*最後に一言。これらはいわゆる「文献調査」です。たった2冊の本でしたが、その主張は微妙に異なっていましたね。
*自分にとって、どちらがより納得するか、という見方はありますが、どちらが正しいとは判断できません。文献調査をする際は、最低でも複数の文献にあたらないと危険です。文献調査で間違ったことをうのみにしてしまうと、そもそも前提から間違った方向に研究が進んでしまう可能性があるからです。
*少なくとも、「諸説あります」くらいの知識がないと、「チコちゃんに叱られますよ!」
・先日の服部先生の授業では、有理数の例として、分数 22/7 がさりげなく登場していましたが、実は深い意味があったようです。世界の「7月22日」は「円周率の日」とされていて、22/7 (22÷7)を計算すると、3.142…となり、円周率の近似値になっています。紀元前250年、ギリシャの数学者アルキメデスが、世界で最初に円周率を計算によって、22/7と求めました。そのことを記念して、7月22日は「円周率の日」と制定されているのです。
円周率は紀元前二千年前から探究されてきましたが、その値は長い間、分数で表されていました。小数が発明されたのは今から400年前に過ぎないのです。
(→ちなみに、日本の「円周率の日」は3月14日。わかりやすすぎますね!)
・ところで、日本では「分数で表すことが出来る数」を「有理数」と呼んでいますが、英語で「有理数」は何と呼ばれているのでしょうか?英訳すると「Rational Number」となるそうです。形容詞「Rational」の名詞形は「Ratio」で、「Ratio」とは「比」を表しています。つまり、形容詞「Rational」は「比なる数」という意味になります。つまり、分数は分子と分母の数の比なので、「比なる数」だというのです。
しかし、それだったら、日本人が「Rational Number」を日本語に訳すとき、「有理数」ではなく「有比数」とすればよかったのではないでしょうか。
(→これって、誤訳だったの?)
・著者は、ここからさらにもう一歩踏み込みます。実は、英語の「Ratio」の起源となったラテン語の「Ratio」には「計算」という意味があるのです。「計算すること」から「比」に通じ、「Rational」は「計算的な」となり「合理的な」になっていきました。そうすると、「Rational Number」の日本語訳の候補として、「比なる数→有比数」と「合理的な数」すなわち「理が有る数→有理数」の2つあったのに、「有理数」が採用されたことになります。なぜ、後者に軍配があがったのでしょうか?
(→さすがはサイエンス・ナビゲーターですね。理詰めで畳みかけてきます。)
・「ピタゴラスの定理」で有名な、古代ギリシャの数学者ピタゴラス(紀元前6世紀頃)は、「万物の根源は数なり」と言ったと伝えられています。この「数」とは自然数(正の整数)のことです。ピタゴラスの時代、自然数こそが計算できる数、つまり「理性の象徴」というべき存在ととらえられていました。分数は、二つの自然数の比として考えられる(計算できる)数に他ならず、そうでない数は「非合理的な」という意味となり、排斥されるべき「考えてはいけない存在」だったというのです。そうした歴史的な背景を考慮し、「Ratinal Number」を「有理数」と訳したのではないか、というのが著者の説です。
(→なるほど、説得力ありますね)
・一方、「無理数」の概念は、もっと後になってから出てきます。現代では、√2やπ(円周率)が無理数であることは知られています。しかし、無理数であること(=分数では表すことが出来ないこと)を証明することは、そう簡単ではありませんでした。円周率πが無理数であることが証明されたのは1761年になってからのことでした。400年前、小数点が発明されたことで、ようやく分数を超えて「無理数」への挑戦が始まったのです。
(→確かに、有理数と無理数はセットになっていますので、「無理数」が存在することがわかって、初めて「有理数」という概念が生じてきたのですね。)
・無理数の英訳は「Irrational Number」で、打消しの接頭語Irがついているので、「比に非ず」と「非合理的」の意味があります。この英語を始めて日本語に訳した昔の日本人数学者は、「非合理的」を採用して、「無理」という言葉をあてたのではないか。
(→個人的には、著者の考えに深く納得しました。)
②一松 信「数の世界」からわかったこと
・こちらの著者は、「有理数」について、以下のように断言します。
「ピタゴラスは半ば伝説的な人物ですが、その伝統もあって古代ギリシャでは当初すべての数は互いに整数の比で表わされる、つまり整数の比で表される分数だけで十分と考えていました。今日では整数の比で表される数を「有理数」といいます。これはRational Number の訳語ですが、原義は「ratio(比)をもつ数」の意味で、むしろ「有比数」と呼ぶのが的確でした。しかし、すでにこの語が定着しているので、厳格にいえば「誤訳」ですがそのまま使います。」と述べています。
(→つまり、昔の日本人数学者が訳した言葉なので、なぜそのように訳したのかを詮索してもしようがない。それは、学問的にはさして重要なことではない。ということでしょうか。なるほど、学者としては、そのように考えるものなのかもしれませんね。)
・しかし、この本には、√2が無理数であることの証明や、なぜ、0.9999999…=1なのか、の証明が詳しく紹介されています。先日の服部先生の授業では、0.9999999…=1が正しいのかどうかわかりませんでしたが、この本では、0.99999999…=1 であることを証明しています。てっきり間違いだと思っていましたが、数学的に正解でした。それを知れただけでも、この本を読んだ価値がありました。
(→もっとも、全部は読んでませんけどね。興味あるところだけです。文献調査をする際は全部読む必要は全くありません。)
*最後に一言。これらはいわゆる「文献調査」です。たった2冊の本でしたが、その主張は微妙に異なっていましたね。
*自分にとって、どちらがより納得するか、という見方はありますが、どちらが正しいとは判断できません。文献調査をする際は、最低でも複数の文献にあたらないと危険です。文献調査で間違ったことをうのみにしてしまうと、そもそも前提から間違った方向に研究が進んでしまう可能性があるからです。
*少なくとも、「諸説あります」くらいの知識がないと、「チコちゃんに叱られますよ!」
①桜井 進「面白くて眠れなくなる数学」からわかったこと
・先日の服部先生の授業では、有理数の例として、分数 22/7 がさりげなく登場していましたが、実は深い意味があったようです。世界の「7月22日」は「円周率の日」とされていて、22/7 (22÷7)を計算すると、3.142…となり、円周率の近似値になっています。紀元前250年、ギリシャの数学者アルキメデスが、世界で最初に円周率を計算によって、22/7と求めました。そのことを記念して、7月22日は「円周率の日」と制定されているのです。
円周率は紀元前二千年前から探究されてきましたが、その値は長い間、分数で表されていました。小数が発明されたのは今から400年前に過ぎないのです。
(→ちなみに、日本の「円周率の日」は3月14日。わかりやすすぎますね!)
・ところで、日本では「分数で表すことが出来る数」を「有理数」と呼んでいますが、英語で「有理数」は何と呼ばれているのでしょうか?英訳すると「Rational Number」となるそうです。形容詞「Rational」の名詞形は「Ratio」で、「Ratio」とは「比」を表しています。つまり、形容詞「Rational」は「比なる数」という意味になります。つまり、分数は分子と分母の数の比なので、「比なる数」だというのです。
しかし、それだったら、日本人が「Rational Number」を日本語に訳すとき、「有理数」ではなく「有比数」とすればよかったのではないでしょうか。
(→これって、誤訳だったの?)
・著者は、ここからさらにもう一歩踏み込みます。実は、英語の「Ratio」の起源となったラテン語の「Ratio」には「計算」という意味があるのです。「計算すること」から「比」に通じ、「Rational」は「計算的な」となり「合理的な」になっていきました。そうすると、「Rational Number」の日本語訳の候補として、「比なる数→有比数」と「合理的な数」すなわち「理が有る数→有理数」の2つあったのに、「有理数」が採用されたことになります。なぜ、後者に軍配があがったのでしょうか?
(→さすがはサイエンス・ナビゲーターですね。理詰めで畳みかけてきます。)
・「ピタゴラスの定理」で有名な、古代ギリシャの数学者ピタゴラス(紀元前6世紀頃)は、「万物の根源は数なり」と言ったと伝えられています。この「数」とは自然数(正の整数)のことです。ピタゴラスの時代、自然数こそが計算できる数、つまり「理性の象徴」というべき存在ととらえられていました。分数は、二つの自然数の比として考えられる(計算できる)数に他ならず、そうでない数は「非合理的な」という意味となり、排斥されるべき「考えてはいけない存在」だったというのです。そうした歴史的な背景を考慮し、「Ratinal Number」を「有理数」と訳したのではないか、というのが著者の説です。
(→なるほど、説得力ありますね)
・一方、「無理数」の概念は、もっと後になってから出てきます。現代では、√2やπ(円周率)が無理数であることは知られています。しかし、無理数であること(=分数では表すことが出来ないこと)を証明することは、そう簡単ではありませんでした。円周率πが無理数であることが証明されたのは1761年になってからのことでした。400年前、小数点が発明されたことで、ようやく分数を超えて「無理数」への挑戦が始まったのです。
(→確かに、有理数と無理数はセットになっていますので、「無理数」が存在することがわかって、初めて「有理数」という概念が生じてきたのですね。)
・無理数の英訳は「Irrational Number」で、打消しの接頭語Irがついているので、「比に非ず」と「非合理的」の意味があります。この英語を始めて日本語に訳した昔の日本人数学者は、「非合理的」を採用して、「無理」という言葉をあてたのではないか。
(→個人的には、著者の考えに深く納得しました。)
②一松 信「数の世界」からわかったこと
・こちらの著者は、「有理数」について、以下のように断言します。
「ピタゴラスは半ば伝説的な人物ですが、その伝統もあって古代ギリシャでは当初すべての数は互いに整数の比で表わされる、つまり整数の比で表される分数だけで十分と考えていました。今日では整数の比で表される数を「有理数」といいます。これはRational Number の訳語ですが、原義は「ratio(比)をもつ数」の意味で、むしろ「有比数」と呼ぶのが的確でした。しかし、すでにこの語が定着しているので、厳格にいえば「誤訳」ですがそのまま使います。」と述べています。
(→つまり、昔の日本人数学者が訳した言葉なので、なぜそのように訳したのかを詮索してもしようがない。それは、学問的にはさして重要なことではない。ということでしょうか。なるほど、学者としては、そのように考えるものなのかもしれませんね。)
・しかし、この本には、√2が無理数であることの証明や、なぜ、0.9999999…=1なのか、の証明が詳しく紹介されています。先日の服部先生の授業では、0.9999999…=1が正しいのかどうかわかりませんでしたが、この本では、0.99999999…=1 であることを証明しています。てっきり間違いだと思っていましたが、数学的に正解でした。それを知れただけでも、この本を読んだ価値がありました。
(→もっとも、全部は読んでませんけどね。興味あるところだけです。文献調査をする際は全部読む必要は全くありません。)
*最後に一言。これらはいわゆる「文献調査」です。たった2冊の本でしたが、その主張は微妙に異なっていましたね。
*自分にとって、どちらがより納得するか、という見方はありますが、どちらが正しいとは判断できません。文献調査をする際は、最低でも複数の文献にあたらないと危険です。文献調査で間違ったことをうのみにしてしまうと、そもそも前提から間違った方向に研究が進んでしまう可能性があるからです。
*少なくとも、「諸説あります」くらいの知識がないと、「チコちゃんに叱られますよ!」
身近な風景
先週は、「栃木県立博物館」のある公園でのアジサイを紹介しましたが、今日はアジサイ寺としても有名な大平山にある「大中寺」のアジサイを紹介します。


境内には、大勢のカメラマンがアジサイの写真を撮っていました。午前中までの雨が上がり、強い日差しを受けたアジサイはとりわけ綺麗に見えました。
いろいろな色や品種?のアジサイが咲いていました。


境内には、大勢のカメラマンがアジサイの写真を撮っていました。午前中までの雨が上がり、強い日差しを受けたアジサイはとりわけ綺麗に見えました。
いろいろな色や品種?のアジサイが咲いていました。






佐高ミュージアム㉗
今回から「佐高ミュージアム研究室だより 」を公開します。
1992年4月から1994年3月までの2年間、佐野高校に在籍しながら、宇都宮大学大学院教育学研究科に内地留学していました。指導教官は、生物学科の中村和夫教授でした。
私は当時、佐野高校の生物部でトウキョウサンショウウオの生態について調査していたので、サンショウウオの生態について研究しようと思っていましたが、中村先生はもともと昆虫生理学が御専門だったので、今まであまり興味のなかった昆虫について研究することにしました。当時の大学院への内地留学は、今と違って、特に教育に関するテーマでなくても、自分のやりたい研究をすることができました。
1992年4月から1994年3月までの2年間、佐野高校に在籍しながら、宇都宮大学大学院教育学研究科に内地留学していました。指導教官は、生物学科の中村和夫教授でした。
私は当時、佐野高校の生物部でトウキョウサンショウウオの生態について調査していたので、サンショウウオの生態について研究しようと思っていましたが、中村先生はもともと昆虫生理学が御専門だったので、今まであまり興味のなかった昆虫について研究することにしました。当時の大学院への内地留学は、今と違って、特に教育に関するテーマでなくても、自分のやりたい研究をすることができました。
当時、宇都宮市内を流れる鬼怒川で、川に生息しているカゲロウという昆虫の一種が、夏の夕方ごろ一斉に羽化し、鬼怒川にかかる橋の水銀灯に集まり、その死骸が数センチにも積り、交通渋滞を引き起こすなど、社会問題となっていました。そこで、この昆虫(アミメカゲロウ)について、研究することにしました。大学院での研究については、追々話が出てきますが、最後には、新種の発見となりました。
この2年間の内地留学期間に、佐野高校の生徒(生物選択者)向けに、「すっかんぽ研究室だより」を20号まで発行しました。佐野高校に原稿を送り、印刷して配ってもらいました。研究室でどんな研究をしているのか、また、同じ研究室の大学院生との調査の様子などを紹介しました。
この2年間は、私のその後の教員人生に大きな転機となりました。高校科学部での研究方法、大学関係の人脈など、科学部指導のノウハウ、後にSGHの探究活動を進める上で必要なことは、すべてこの2年間で学んだといっても過言ではありません。この黄金の2年間で見聞きしたことを高校生向けに紹介した「すっかんぽ研究室だより 全20号」を今回から5号ずつ公開していきます。
(前置きが長くなってしまいました)
佐高ミュージアム 研究室だより No.1 「アミメカゲロウの謎!」.pdf
佐高ミュージアム 研究室だより No.2 「ホタルイカ」.pdf
佐高ミュージアム 研究室だより No.3 「名古屋の八田耕吉先生」.pdf
佐高ミュージアム 研究室だより No.4 「カラスウリの花」.pdf
佐高ミュージアム 研究室だより No.5 「アミメモドキ現われる!」.pdf
中3(数学)の授業見学
本日7限目は、中学3年1組の「数学」(服部先生)の授業を見学しました。
服部先生は、臨時休業中にたくさんの授業動画をアップしていましたね(私が数えてみたら16本ありました!)。独特な登場の仕方で、心を鷲づかみ?された生徒も多かったと聞いています。
今日の学習のめあては、「有理数と無理数について分かる」でした。
①授業はまず、前時の復習で、平方根の大小の確認問題から入りました。
-3 と √10 -0.7 と ー√0.7
(どっちが大きいかわかりますか)
②次がいよいよ本題で、有理数と無理数の違いの説明です。
有理数 → 分数で表すことが出来る数
例:整数、0.3 -1.2 2/3 など
無理数 → 分数で表すことが出来ない数
例:π=3.141592653589793238462643383279
(円周率です。澁江さんは30桁まですらすら答えました!)

服部先生は、臨時休業中にたくさんの授業動画をアップしていましたね(私が数えてみたら16本ありました!)。独特な登場の仕方で、心を鷲づかみ?された生徒も多かったと聞いています。
今日の学習のめあては、「有理数と無理数について分かる」でした。
①授業はまず、前時の復習で、平方根の大小の確認問題から入りました。
-3 と √10 -0.7 と ー√0.7
(どっちが大きいかわかりますか)
②次がいよいよ本題で、有理数と無理数の違いの説明です。
有理数 → 分数で表すことが出来る数
例:整数、0.3 -1.2 2/3 など
無理数 → 分数で表すことが出来ない数
例:π=3.141592653589793238462643383279
(円周率です。澁江さんは30桁まですらすら答えました!)

③無限に続く小数→循環小数と循環しない小数(→だんだん難しくなっていきますね。)
循環小数 → 4/3=1.3333333…
=1.3(3の上に・)
22/7=3.142857142857…
=3.142857(1と7の上に・)
循環しない小数 → π や √2など

④循環小数を分数にする(→そんなことができるの?)
例:0.162(1と2の上に・)
X=0.162 とし、両辺を1000倍し、もとの式を引くと、
1000X=162.162162…
-) X= 0.162162…
999X=162
よって、X=162/999 →約分すると X=6/77
*こんなふうに、循環小数は必ず分数にすることが出来るんですね!
(人生得した気分です。といっても、自分もきっと習っていたはずですけど)
⑤最後に、服部先生からこんな問題が出されました。
Q 循環小数 0.9(9の上に・)を分数にせよ。
A X=0.9… とし、両辺を10倍し、元の式を引くと
10X=9.9…
-) X=0.9…
9X =9
X=1
つまり、循環小数 0.9(9の上に・)=1 となります。
(こんなありえないことが起こってきます。なぜ、こうなるのかはわかりません。いやあ、数学は奥が深いですね!)
*授業はここで終わりました。生徒たちに授業の感想を聞いてみました。
澁江さん「授業はとてもわかりやすかったです。循環小数のことも理解できました。」
渡辺君「服部先生はユーモアがあり、授業がとても楽しみです。」
*最後に私の感想ですが、「有理数と無理数について分かる」という本時のめあては十分達成できていたのではないかと思います。個人的には、そもそも、分数で表すことが出来る「有理数」が示す「理(ことわり?)」とは何なのか?に興味を持ちました。有理数=理にかなった数、何ゆえ、有理数と呼ぶのか知りたい、と強く思いました。数学も面白いですね。
(→こう思わせるのも服部先生のねらいだったのでしょうか? だとしたら、服部先生の思うつぼでしたね。)
循環小数 → 4/3=1.3333333…
=1.3(3の上に・)
22/7=3.142857142857…
=3.142857(1と7の上に・)
循環しない小数 → π や √2など

④循環小数を分数にする(→そんなことができるの?)
例:0.162(1と2の上に・)
X=0.162 とし、両辺を1000倍し、もとの式を引くと、
1000X=162.162162…
-) X= 0.162162…
999X=162
よって、X=162/999 →約分すると X=6/77
*こんなふうに、循環小数は必ず分数にすることが出来るんですね!
(人生得した気分です。といっても、自分もきっと習っていたはずですけど)
⑤最後に、服部先生からこんな問題が出されました。
Q 循環小数 0.9(9の上に・)を分数にせよ。
A X=0.9… とし、両辺を10倍し、元の式を引くと
10X=9.9…
-) X=0.9…
9X =9
X=1
つまり、循環小数 0.9(9の上に・)=1 となります。
(こんなありえないことが起こってきます。なぜ、こうなるのかはわかりません。いやあ、数学は奥が深いですね!)
*授業はここで終わりました。生徒たちに授業の感想を聞いてみました。
澁江さん「授業はとてもわかりやすかったです。循環小数のことも理解できました。」
渡辺君「服部先生はユーモアがあり、授業がとても楽しみです。」
*最後に私の感想ですが、「有理数と無理数について分かる」という本時のめあては十分達成できていたのではないかと思います。個人的には、そもそも、分数で表すことが出来る「有理数」が示す「理(ことわり?)」とは何なのか?に興味を持ちました。有理数=理にかなった数、何ゆえ、有理数と呼ぶのか知りたい、と強く思いました。数学も面白いですね。
(→こう思わせるのも服部先生のねらいだったのでしょうか? だとしたら、服部先生の思うつぼでしたね。)
中3(国語)の授業見学
今日は、中学3年の国語と数学の授業を見学しました。
まずは、中3「国語」(3年3組、5限目)北堀先生の授業です。
本日のテーマは「俳句を作って句会を開こう」です。
句会は、次のような手順で開かれました。
①選句用紙に、グループ(5~6人)で一人一句ずつ、自分の自信作を書いていきます。
②グループ全員の俳句の中から、一番良いと思う句(自分の句以外で)を一つ選びます。
③自分が良いと思った俳句について、なぜそう思ったのかをグループ内で発表し合います。
④最も票を集めた俳句を班の代表として黒板に書き、発表します。

自分が良いと思った俳句となぜそう思ったかを発表し合っています。
まずは、中3「国語」(3年3組、5限目)北堀先生の授業です。
本日のテーマは「俳句を作って句会を開こう」です。
句会は、次のような手順で開かれました。
①選句用紙に、グループ(5~6人)で一人一句ずつ、自分の自信作を書いていきます。
②グループ全員の俳句の中から、一番良いと思う句(自分の句以外で)を一つ選びます。
③自分が良いと思った俳句について、なぜそう思ったのかをグループ内で発表し合います。
④最も票を集めた俳句を班の代表として黒板に書き、発表します。

自分が良いと思った俳句となぜそう思ったかを発表し合っています。

各班で選ばれた俳句を黒板に書いています。

各班の代表作が出そろいました。
それぞれの俳句について、作者の説明を聞き、一番良いと思った俳句を選びました。
1班「梅雨時の 照れる旭と 君の声」
2班「雨が降り 水たまりには 未来像」
3班「寒椿 待ち人いずこ 白い息」
4班「休校中 一時帰宅する 母ツバメ」
5班「猛暑日の 部屋の空気は 赤道下」
6班「制服や 引きこもり吹く 夏の風」
さて、皆さんだったらどれがいいですか?
ちなみに、私は生き物好きなので、生き物が詠み込まれている俳句には反応してしまいます。「生き物」俳句にはこんな作品もありました。
「晴れぬ気と 天気をながめる あまがえる」
「触覚を ゆうゆう伸ばす かたつむり」
*生徒の今日の感想より
「俳句を作るのがこんなに楽しいとは思っていませんでした。」
「自分で見つけた驚きや感動を俳句にすることで、言葉のセンスや想像力が高められました。」
「17音で色々な思いを伝えることができるのはすごいなと思いました」
「俳句には人それぞれの個性が表れていることがわかりました」等
*本時は、確かに楽しい句会でした。自分が選んだ俳句と選んだ理由を語り合う場面が一番盛り上がっていました。楽しいなあ、と言う声もあちこちで聞こえてきました。みんなそれぞれこだわりがあって、なかなか一つに決まらないところが良かったです。
ちょっとのぞいてみようと軽い気持ちで、見学を始めましたが、面白くなって、結局、最初から最後まで見学しました。
高1CTPの授業見学
今日の7限目は、高校1年生のCTP(Criticai Thinking Program)の授業を見学しました。高1の1組から4組まで、同じ時間帯で授業を受けています。
CTPは「批判的な思考力」を養う本校独自の学校設定科目で、国語科、数学科、理科、地歴公民科、英語科の各教員がチームとなって授業を行う合科授業です。1年間の前半は、国語科、数学科、理科、地歴公民科、それぞれの教科で「批判的な思考力」を養う教材を作成し、その教科の教員の指導の下に授業を行います。後半は、それまでに身につけた「批判的な思考力」を活用し、英語科が中心となった「ディベート活動」を行います。
今日は、地歴公民科の島田先生が作成した教材「見えているものが真実とは限らない」と題した授業を行いました。


(浜島書店「最新図説 政経」を参考に作成。授業のパワーポイント資料より)
CTPは「批判的な思考力」を養う本校独自の学校設定科目で、国語科、数学科、理科、地歴公民科、英語科の各教員がチームとなって授業を行う合科授業です。1年間の前半は、国語科、数学科、理科、地歴公民科、それぞれの教科で「批判的な思考力」を養う教材を作成し、その教科の教員の指導の下に授業を行います。後半は、それまでに身につけた「批判的な思考力」を活用し、英語科が中心となった「ディベート活動」を行います。
今日は、地歴公民科の島田先生が作成した教材「見えているものが真実とは限らない」と題した授業を行いました。


(浜島書店「最新図説 政経」を参考に作成。授業のパワーポイント資料より)
昨年度は、1学年全員が格技場で一斉に授業を受けていましたが、その形態だとメモがとりにくかったり、グループワークなどがしにくいことや、コロナや熱中症対策で、今年度は各教室で実施しました。
教材作成者の島田先生が、担任をしている1年3組で授業し、それをZoomを使って、他の3クラスに同時中継することで、4クラスの一斉授業が可能になりました。

1年3組で授業をする島田先生

他の3クラスでは、Zoomによって配信された画面を見ながら学習します。
生徒に授業を受けた感想を聞いてみました。
まずは、島田先生の授業をその場で受けた3組の生徒です。
林さん「事実や根拠の意味、日常生活との関わりなど、これからどうやって生活していけばいいのか考えるきっかけとなりました。」
小林さん「前提、根拠など、具体的な事例が紹介されていたので、わかりやすかったです。」
松本君「固定観念にとらわれない考え方が大切だとわかりました。興味を持てる内容だったので、面白かったです。」
それでは、Zoomによる遠隔授業を受けていた生徒たちはどうだったでしょうか。
新井さん「音の大きさが突然変わることがありましたが、遠隔でも普通に授業を受けているのと変わりありませんでした。」同様多数。
*島田先生が伝えたいことは、遠隔でもしっかりと生徒たちに伝わっていました。
中3英語の授業見学
今日も、いろいろな先生の授業を見学しました。
中学3年3組の「英語」(高木先生)の授業です。
昨日の高校3年生の英語の授業を見学し、中学校ではどんな授業をしているのか興味を持ちました。
3限目に英語演習室で行われている「英語」の授業を見せてもらいました。
・Lesson 3「Rakugo Goes Overseas」(世界に広がる落語)は、英語で落語を行う大島希巳江(おおしま きみえ)さん、桂三輝(かつら さんしゃいん)さんが登場します。

桂三輝(かつら さんしゃいん)さんの落語。カナダ出身のプロの落語家です。
中学3年3組の「英語」(高木先生)の授業です。
昨日の高校3年生の英語の授業を見学し、中学校ではどんな授業をしているのか興味を持ちました。
3限目に英語演習室で行われている「英語」の授業を見せてもらいました。
・Lesson 3「Rakugo Goes Overseas」(世界に広がる落語)は、英語で落語を行う大島希巳江(おおしま きみえ)さん、桂三輝(かつら さんしゃいん)さんが登場します。

桂三輝(かつら さんしゃいん)さんの落語。カナダ出身のプロの落語家です。
・教科書の内容を学習した後、「マッピング」という作業を行います。教科書に書かれていることを参考にして、例えば、「Rakugo」に関する情報をプリントに書き出します。その際、教科書以外の内容や自分の感想なども記入し、「Rakugo」に関することが一目でわかる「マップ」を作成します。
・このマップをもとに、「Rakugo」について伝えるストーリーを英語で作ります。これが、Story Retelling(ストーリー リテリング)です。自分が作ったストーリーを英語で相手に伝え、さらに相手を変えて繰り返すことで、他の人のアイディアを取り込み、ストーリーをより魅力的なものにしていきます。こうして英語での表現の幅がどんどん広がっていく、という画期的な取組です。



授業が終わった後に生徒に感想を聞いてみました。
落合さん「他の人が話すストーリーを聞いて、そういうストーリーもあるのかと勉強になりました。」
山口さん「英語でのコミュニケーションがたくさんできて楽しかったです。」
清水君「日本の文化を英語で伝えることは難しかったです。しかし、ジェスチャーを交えれば何とか紹介できるんじゃないかと思いました。」
*生徒たちは、ペアワークを繰り返すことで、ペアの相手の発想の良さに気づいたり、それを取り入れて自分の表現の幅がひろがったことに喜びを感じたり、コミュニケーションの楽しさを感じていたりしていました。 素晴らしい授業です!
高3理系(英語)の授業見学
本日、3限目、高校3年生理系の「コミュニケーション英語Ⅲ」(川俣先生)の授業を見学しました。
教科書のLesson2「God's Hands(神の手)」を教材に、授業を進めていました。
Lesson 2は、「神の手を持つ」と言われ、2012年に当時の天皇陛下の心臓バイパス手術を執刀した心臓外科医、天野篤(あまの あつし)さんを取り上げています。天野さんは、順天堂大学医学部心臓血管外科教授として、また同大学医学部附属順天堂医院院長として、現在も第一線で活躍しています。
この教材をもとに、授業は物語のSection(段落)ごとに、以下のように進められていました。
Step1.発音の確認。:単語やフレーズの発音を確かめ、CDや教員のあとに続いて発音。CDを聞いてListening Quiz に答える。等
Step2.本文を読む。:文章の構造を理解し、正確に文章を理解する。
Step3.Q&A:ペアに分かれて問題を出し合う、音読穴埋め:適語を補いながら音読する。 ←(本時はここまで)
Step4.サイトラ(Sight translation):英文または日本文を見て、それぞれを翻訳する。
教科書のLesson2「God's Hands(神の手)」を教材に、授業を進めていました。
Lesson 2は、「神の手を持つ」と言われ、2012年に当時の天皇陛下の心臓バイパス手術を執刀した心臓外科医、天野篤(あまの あつし)さんを取り上げています。天野さんは、順天堂大学医学部心臓血管外科教授として、また同大学医学部附属順天堂医院院長として、現在も第一線で活躍しています。
この教材をもとに、授業は物語のSection(段落)ごとに、以下のように進められていました。
Step1.発音の確認。:単語やフレーズの発音を確かめ、CDや教員のあとに続いて発音。CDを聞いてListening Quiz に答える。等
Step2.本文を読む。:文章の構造を理解し、正確に文章を理解する。
Step3.Q&A:ペアに分かれて問題を出し合う、音読穴埋め:適語を補いながら音読する。 ←(本時はここまで)
Step4.サイトラ(Sight translation):英文または日本文を見て、それぞれを翻訳する。
この授業の進め方は、担当の先生が変わると教え方ががらっと変わってしまうのではなく、担当の先生が違っても同じ内容を学習できるよう、本校の英語科の先生方が試行錯誤しながら、たどり着いた「学習サイクル」だそうです。このサイクルの中で、それぞれの先生が工夫してプリントを作ったりしています。これによって、本校の英語科全体の指導力アップにつながりました。
(以上は、授業後に英語科の先生方にお聞きした内容をもとにまとめました。もし間違っていたら後で訂正します。)


写真は、Step3の「Q&A」に取り組んでいる生徒たちです。
授業終了後、近くにいた生徒に授業の感想を聞いてみました。
中野君「いつも通りの川俣先生の授業です。先生の説明を一方的に聞くのではなく、ディスカッションがあり、話し合い活動が多いので、眠くなるようなことはありません。」
入澤君「ペアワークが多いです。単語やフレーズの発音を自分で確認できるところがよいと思います。」
岡さん「先生が元気すぎるので疲れますが、眠くなりません。」
*川俣先生のパワー溢れる授業が印象的でした。授業見学は、突然、ふらっとお邪魔しましたが、一見して生徒が授業に真剣に楽しく取り組んでいることがわかりました。
中2(華道)、中1(学活)の授業見学
今日の7限目に、
①中学2年1組の「華道」(総合的な学習の時間)の授業と
②中学1年生の「学活」(総学の振り替えにより実施)の授業を見学しました。
①「華道」の授業では、小原流の清水一克先生のご指導により、生徒一人一人が、実際にお花を生け、最後に清水先生に手直し等をしていただき、作品を完成させます。今日は、ニューサイラン、カスミソウ、カーネーションの3種を使いました。


生け方には、いくつかの型があるそうで、それをもとに生徒たちは何度も試行錯誤をしながら、完成させていました。
①中学2年1組の「華道」(総合的な学習の時間)の授業と
②中学1年生の「学活」(総学の振り替えにより実施)の授業を見学しました。
①「華道」の授業では、小原流の清水一克先生のご指導により、生徒一人一人が、実際にお花を生け、最後に清水先生に手直し等をしていただき、作品を完成させます。今日は、ニューサイラン、カスミソウ、カーネーションの3種を使いました。


生け方には、いくつかの型があるそうで、それをもとに生徒たちは何度も試行錯誤をしながら、完成させていました。
何人かの生徒に感想を聞いてみました。
浅野さん「茎が細いカスミソウは指しにくかったです。正面だけでなく、横から見たときにも立体感を出すのが難しかったです。とても楽しかったです。」
恩田さん「初めてだったので難しかったです。緊張しました。最初は、何が良くて何が悪いのかわかりませんでしたが、先生に直していただくと、なるほどそうなのかと納得しました。先生からは90点と言われました。」

お花は、家に持ち帰り、家でもう一度、生けてみるそうです。
自分でお花が生けられるなんて、素敵ですね。
②中学1年生は、7限目に「学活」を行いました。
テーマは「ソーシャルスキル」、ソーシャルディスタンスではありませんよ。
友人関係のスキルを身につけます。
私たちは、何かを失敗したときに「ごめんなさい」と謝りますが、そのタイミングを逸してしまい、後悔した経験は誰しもあると思います。
ソーシャルスキルは、これまで謝れなかった自分の経験を振り返り、場面に応じた謝罪の仕方を確認します。
2人1組になり、「さりげない謝罪」「普通の謝罪」「丁寧な謝罪」を表す言葉や態度を考え、実際にやってみました。
最後に、我こそはと思う生徒が、担任の先生を相手に、「さりげない謝罪」、「普通の謝罪」、「丁寧な謝罪」にチャレンジしていました。

「さわやかに謝ることができる佐附中生」、もうそれだけで素晴らしいです!
緊急情報
特にありません。
カウンター
0
9
8
6
0
0
1
6







