文字
背景
行間
校長室便り
高3・フードデザインの授業見学
今回のメニューは「春巻き(6本)、ほうれん草とツナのポン酢あえ」です。

今日の授業は、まず、春巻きやほうれん草に関する学習から始まりました。
春巻きには、中国料理とベトナム料理があり、それぞれ使う皮が違いますが、今回は中国料理の春巻きを作ります。

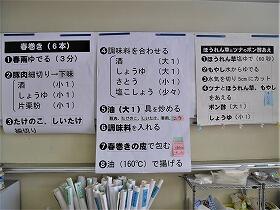
「春巻き」の料理で、ポイントとなるのは、具を春巻きの皮で包むところだそうです。きれいに包めれば、それだけ見栄えや食感もよくなります。まずは、具となる、春雨(ゆでる)、豚肉(下味をつける)、たけのこ・しいたけ(ほそぎり)、ニラを炒め、調味料で味付けします。


生徒たちの包丁さばきや炒め方も手慣れたものになってきました。


そして、いよいよ今回のポイントである、春巻きの皮で具を包みます。


くっついている皮をはがす作業も重要です。


皮の包み方もやっているうちにうまくなってきます。


おいしそうに揚がっています。
ほうれん草とツナのポン酢あえも完成し、お楽しみの試食タイムです。




最後に、生徒の感想を聞いてみました。
「今回の料理では、春巻きを巻くところが一番難しかったです。でも、やっているうちにコツがつかめてきました。」
「具のタケノコがいい食感です。おいしくできました。」
「春巻きの揚がり具合がちょうどいいです。パリッとした食感がたまりません。」
「思ったより簡単にできたのでびっくりしました。家でも作ってみたいです。」
*皆さんの自己評価は非常に高く、春巻きを頬張る姿からは、満足感、達成感が感じられました。調理実習は、究極のアクティブラーニングだと思います。
ボート部全国大会~下野新聞掲載
8位入賞となった藤倉さん、木村さんのインタビュー記事が載っています。

(2020年9月29日付け下野新聞18面掲載、掲載許諾済)
ボート2020.9.29.pdf
身近な風景 ~中秋点描

アキアカネが稲穂の周りを飛んでいました。
佐野市では、古代米を栽培しているところがあるようです。佐野市富士町で見かけました。


古代米とイナゴ
ソバの白い花が青空に映えています。


真っ赤なヒガンバナに交じって、薄いピンクの花も時々見かけました。


場所によっては、ヒガンバナはまだ蕾も多かったです。


田んぼの土手のヒガンバナが満開になると、稲穂(黄)、ソバ(白)、ヒガンバナ(赤)、その他(緑)と、色とりどりになりますね。来週が楽しみです。
身近な風景 ~ヒガンバナ③四~六分咲き

↓ さて、今日(27日)はどうなっているでしょうか。
9月27日(日)、校庭前庭のヒガンバナは四分咲きくらいです。




佐野高校では、前庭以外でもヒガンバナが咲いている場所が他にもありました。

西門近くの部室棟の近くです。四分咲きくらい。

寮の前の駐車場の角です。
佐野でヒガンバナの名所の一つである三毳山公園内にある「万葉庭園」に行ってきました。




綺麗に咲いている場所もありましたが、全体としては、まだ四~六分咲きといったところです。10月に入った頃から来週末(10月3日,4日)くらいが満開ではないでしょうか。その時の風景が楽しみです。
「女子セブンスユースアカデミー」秋田若菜さん
9月19日、日本ラグビー協会は、22日と27日に行われる「女子セブンスユースアカデミー」の参加選手を発表しました。高校3年2組の秋田若菜さんを始めとする、アカデミー生(10名)と候補生(15名)が選ばれました。秋田さんは、高校1年の時から連続して選ばれています。

昨年12月27日に大阪花園ラグビー場で開催された「U18花園女子15人制大会」に東軍として参加した時の写真です。(石井先生撮影)
「女子セブンスユースアカデミー」は、世界と戦える可能性を秘めた人材をユース世代から発掘し、育成・強化に取り組むプログラムで、多くの日本代表選手を育ててきました。
秋田さんは、昨年の「太陽生命ウィメンズシリーズ」でチャレンジチームの主将を務めており、2024年のパリオリンピックを目指す若手「女子セブンスユースアカデミー」の中心メンバーでもあります。23日、本人から話を聞かせてもらいました。

Q9月22日に行われた「アカデミー」では、どんなことをやったのですか?
本来なら、全員がそろって活動をするのですが、新型コロナの影響で、すべてズームを使った遠隔で行なわれました。9時から15時まで、各1時間のプログラムを4コマ受講しました。以下のような内容でした。
1コマ目:「コミュニケーションゲーム」(ほぼ6ヶ月ぶりに仲間とコミュニケーションをとることができました。
2コマ目:「SアンドC(ストレンクス(筋トレ)とコンディショニング)」、(どういう筋トレをすればいいのか、目標値を設定します)
3コマ目:「ラグビーのスキルの研究」(海外の選手のプレーを見て、プレースタイルなどについて話し合います)
4コマ目:「オリンピックについて学ぶ」(オリンピックに出るためには、まず、オリンピックについて知ることが重要です。)
Q「アカデミー」に参加して、どんなことを感じましたか?
今回は、ズームでの参加でしたが、仲間と会うのは久しぶりだったので、コミュニケーションの大切さを再認識しました。また、オリンピックという目標に向けての気持ちや今できることを共有できたことが大きかったです。
*現在、秋田さんは、クラブチーム「アルカス熊谷」に所属して、練習しています。「女子セブンスユースアカデミー」は、高3の12月までですので、さらに上部団体である「女子SDS(セブンズ・ディベロップメント・スコッド)」に選抜されることを目標にしているそうです。
新型コロナの影響で練習や試合にはまだ様々な制約がありますが、2024年のパリオリンピックを目指して、頑張ってください。応援しています。
特にありません。







